Our goal is to study the complexity of convergence schemes and their limits. Sequences
(viewed as evolutions) with the absorption property lead to so-called generic objects. One
of our objectives is to extend this study in several directions. We are also going to analyze
convergence schemes in which there are no evolutions with the absorption property, where
the set-theoretic forcing plays a pivotal role.

Introduction

Let us imagine that a certain evolution system is given, starting from some initial state $E_0$ and having the property that for every two transitions $f$, $g$ from the same state $Z$ it is possible to make two further transitions $f^{\prime }$, $g^{\prime }$ so that the compositions $f^{\prime }f$ and $g^{\prime }g$ are the same, in particular, leading to the same state. It is then natural to expect that there exists a special infinite process accumulating all possible states and in some sense absorbing all possible transitions. Specifically, denoting a fixed transition $f$ from $A$ to $B$ by $A\stackrel{f}{\to }B$, an infinite process (evolution) can be represented as an infinite diagram of the form

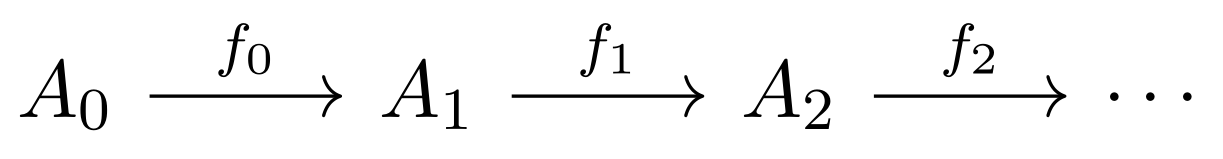
where $A_0=E_0$. Saying that such a process absorbs all possible transitions means that for every $n$, given a transition $A_n\stackrel{f}{\to }Y$, there exist $m>n$ and a transition $Y\stackrel{g}{\to }{A}_m$ such that the composite transition $f_{m-1}\dots <!--\; FUNCTION\; APPLICATION\; -->f_n$ is the same as $\mathit{gf}$ or at least approximates $\mathit{gf}$ with a given in advance error. It turns out that if a process with the absorption property exists, it is essentially unique and may be called generic. This means that every two processes with the absorption property are isomorphic, which in turn means that there is a way of “jumping” between the first and the

second one infinitely many times.

It is rather evident that the proper framework for describing and studying such evolution systems comes from category theory. Namely, the objects are the system states while the arrows are transitions. Category theory offers here elegant and quite strong, yet at the same time manageable, tools to be utilized. Perhaps one of the basics is the concept of a functor. In order to describe an infinite transition process (evolution), it suffices to use functors from the set of non-negative integers $\omega$ (more traditionally denoted by $\mathbb{N}$) viewed as a category in which the objects are natural numbers and arrows are pairs of the form $⟨n,m⟩$ with $n\le m$.

Actually, a significant power of category theory lies within the notion of colimit of a functor, unifying concepts like supremum in partially ordered sets, Cartesian products, unions of families of structures, and so on. In particular, every functor from the natural numbers has its colimit in a suitable, possibly bigger, category.

While it is possible to investigate evolution processes in their “pure” form, it is usually more convenient and more natural to look at their colimits, identifying them with the isomorphism classes of certain objects of a bigger category.

In this way we arrive at the basic concept of this project: abstract convergence scheme, namely a category $𝔎$ embedded into a category $\mathit{\sigma 𝔎}$ consisting of limits of sequences from $𝔎$. Here, the “limit” may be either as “colimit” in the category-theoretic sense or some more general operator acting on certain sequences, possessing the main properties of colimits.

Abstract convergence schemes

By an abstract convergence scheme we mean a triple $\left(𝔎,\mathit{\sigma 𝔎},\lim <!--\; FUNCTION\; APPLICATION\; -->\right)$, where $𝔎$ is a category, $\mathit{\sigma 𝔎}\supseteq 𝔎$ is a bigger category, $\lim <!--\; FUNCTION\; APPLICATION\; -->$ is an operator assigning to some sequences in $𝔎$ (or, more generally, covariant functors from some directed posets into $𝔎$) their co-cones in $\mathit{\sigma 𝔎}$, pretending to be their colimits. There is a short list of natural axioms (in the spirit of Hausdorff convergence of sequences of points) making this structure sound and meaningful. In most cases, $\lim <!--\; FUNCTION\; APPLICATION\; -->$ is the colimit in the category-theoretic sense. An example of a convergence scheme may be a partially ordered set $P$, with $\mathit{\sigma P}$ being the set of all ideals generated by increasing sequences in $P$ (we identify $p\in P$ with the ideal generated by $p$). Then $\lim <!--\; FUNCTION\; APPLICATION\; -->\left(x_n\right)$ is simply the ideal generated by the sequence $\left(x_n\right)$. Many natural examples come from model theory, where $𝔎$

is a category of finite (or finitely generated) models of a fixed first-order language with embeddings as arrows, while $\mathit{\sigma 𝔎}$ is the category of all models isomorphic to unions of countable chains in

$𝔎$, again with embeddings as arrows.

Now $\lim <!--\; FUNCTION\; APPLICATION\; -->\left(x_n\right)$ is isomorphic to the union (formally: colimit) of the chain $\left(x_n\right)$, as embeddings can always be replaced by inclusions).

Given a concrete convergence scheme, one has to first consider whether any interesting $\mathit{\sigma 𝔎}$-object occurs as the “limit”. If so, then there is a chance that, up to isomorphism, a “special’ object occurs “most frequently”. Of course, this needs to be made precise, either by finding a reasonable topology on the objects of $\mathit{\sigma 𝔎}$, where “occurring frequently” means forming a non-meager or even a co-meager set. Another option is to find a reasonable probability measure on the objects of $\mathit{\sigma 𝔎}$, where “occurring frequently” would mean “with positive probability” or even “with probability one”. A more abstract approach would require considering some ideal of “small” sets whose complements are therefore called “large”. Actually, a quite common word for “occurring most frequently” or “typically” is “being generic”. This name has been used in the theory of set-theoretic forcing (generic filters) and from time to time is used in descriptive set theory, when considering a complete topological space whose elements could have various properties. Thanks to the Baire category theorem, we can say that a fixed property is generic if elements without this property form a meager set. In the project we are going to explore the concept of being generic in abstract convergence schemes.